関数の特徴は xの値を定めると、yの値が１つだけ決まる ことにあります。
y = 2x + 1（式）
xの値を決めると→yの値が決まる
：→：
：→：
-2→-3
-1→-1
0→1
1→3
2→5
3→7
：→：
：→：


上の（xの値）と（yの値）のペアをそれぞれ、x座標 と y座標 として１点ずつ、xy座標平面に打点します。
この作業をすることによって、式が絵に替わるのです。

y = 2x + 1（式） 　　　
xの値を決めると →yの値が決まる→打点グラフ（絵）
：→：→：
：→：→：
：→：→：
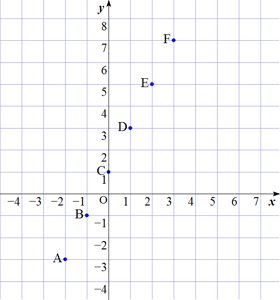
-2→-3→A (-2, -3)
-1→-1→B (-1, -1)
0→1→C (0, 1)
1→3→D (1, 3)
2→5→E (2, 5)
3→7→F (3, 7)
：→：→：
：→：→：
：→：→：
↑
x座標の値 とする		　↑
y座標の値 とする		　↑
点の座標		　


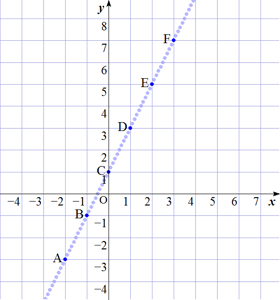
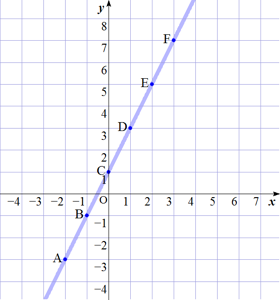
x の値を 1.0刻み から、0.1刻み、0.01刻み、0.001刻みと細かくしていくと、点が連続となります。
x の値を 1.0刻み にした場合x の値を 0.1刻み にした場合x の値を 0.01刻み にした場合


「なぜ、これらの点の集合が直線になるか」については、「三角形の相似」の学習が終わるのを待たなくてはなりませんが、表中の 「xの数値 の増加量」と 「yの数値 の増加量」の比 が、「グラフ中のどのようなこととなって現れているか」を考えると、理解できます。

＊ 説明が長くなりますので、ここでは、「直線になる理由」の具体的な教え方は割愛することに致します。


「直線 y = ax + b が(2, 5)を通るとき・・・」という言葉があると、多くの生徒さんたちは条件反射的に「5 = 2a + b」と書きます。しかし、なぜこの等式が成り立つのかに疑問を持つ生徒さんはほとんどいません。

上述のことを理解していますと、「直線 y = ax + b が(2, 5)を通るとき・・・」という言葉は、「y = ax + b の式の xの値 を 2 に定めると、yの値 は 5 となる。」という意味であることがわかりますので、5 = 2a + b という等式が成り立つことになります。